2. Формулы для площади равнобедренной трапеции с вписанным кругом
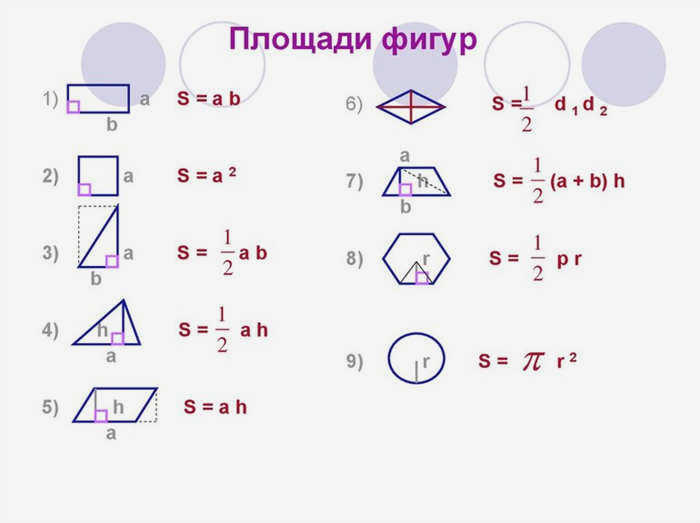
Формула площади геометрической фигуры
– это числовая характеристика геометрической фигуры, которая показывает размер фигуры (площадь, заключенная в контуре фигуры). Площадь выражается в количестве квадратных единиц.
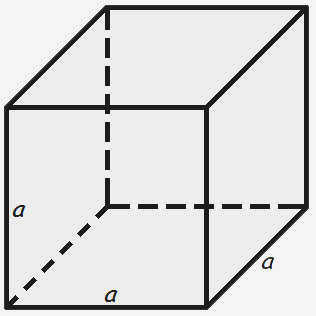
Площадь куба равна квадрату длины его стенки, умноженному на шесть.
Формула для площади куба имеет вид:
S = 6 a 2
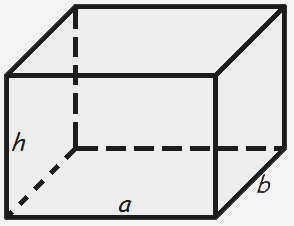
Где S – площадь поверхности куба,
a – длина стенки куба.
Площадь цилиндра
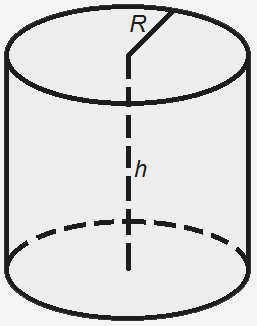
Площадь стороны кругового цилиндра равна произведению периметра основания и высоты.
Формула для вычисления площади боковой стороны цилиндра:
S = 2 π R h
Общая площадь поверхности кругового цилиндра равна сумме площади боковой поверхности цилиндра и площади его основания.
Формула для вычисления общей площади цилиндра:
S = 2 π R h + 2 π R 2 = 2 π R ( R + h )
Где S – площадь поверхности,
R – радиус цилиндра,
h – высота цилиндра,
π = 3.141592.
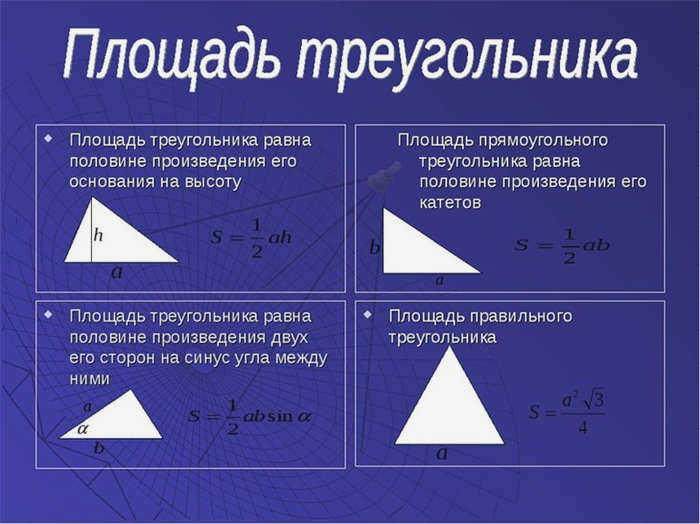
Площадь треугольника со стороной и двумя углами, формула.

a , b , c – стороны треугольника
α , β , γ – противоположные углы
Площадь треугольника по стороне и двум углам (S):
Формулы для площади треугольника:
Площадь треугольника, формула Герона
Зная длины всех трех сторон
и используя формулу Герона, мы можем найти площадь неправильного треугольника
a , b , c – стороны треугольника
p – луч, p=( a + b + c )/2
Формула ( Герон ) для площади треугольника через полукруг ( S ):
Калькулятор – вычислить, найти площадь треугольника:
Формулы для площади треугольника:
Площадь треугольника с тупым углом
h – высота треугольника a – основание
Формула для площади треугольника с расширением (S): Формула для площади треугольника:
Зная две стороны и синус угла между ними, находим площадь треугольника по формуле a , b , c – стороны треугольника α , β , γ – углы Формулы для площади треугольника через две стороны и угол между ними (S): Калькулятор – вычислить, найти площадь треугольника: Формулы для площади треугольника: Стороны разветвленного треугольника Стороны равнобедренного треугольника Стороны прямоугольного треугольника Высота разветвленного треугольника Высота, медиана, биссектриса равнобедренного треугольника Высота=медиана= биссектриса равнобедренного треугольника Биссектриса разветвленного треугольника Медиана разветвленного треугольника Медиана прямоугольного треугольника Все геометрические единицы
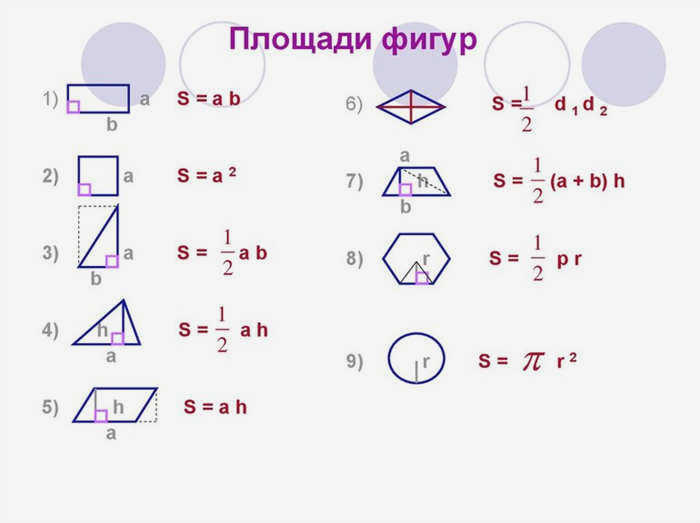
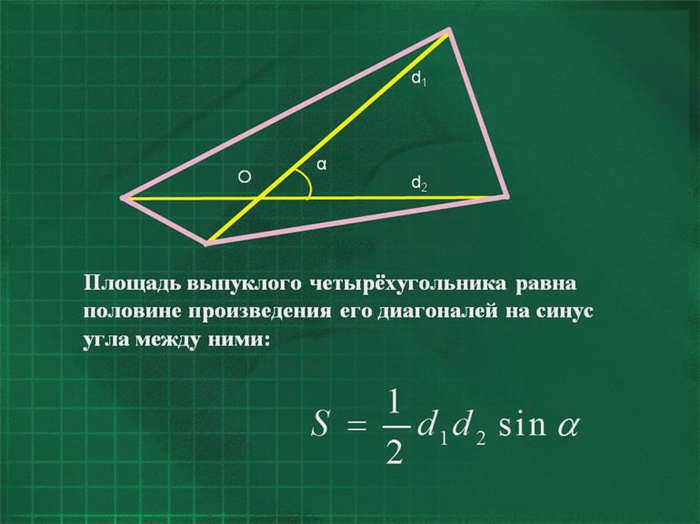
Площадь четырехугольника
Четырехугольник – это одна из геометрических фигур (многоугольник), имеющая четыре стороны и четыре вершины, три из которых не лежат на одной прямой. Четырехугольник называется выпуклым, если он с одной стороны лежит на прямой, которая является продолжением любой из его сторон.
К выпуклым четырехугольникам относятся почти все известные фигуры с четырьмя вершинами и четырьмя сторонами. Их основными типами являются: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.
Квадрат и прямоугольник
Самый простой способ вычислить площадь квадрата – умножить сторону на себя, другими словами, возвести в квадрат длину любой из его сторон (S = a 2 ). Такое вычисление связано с особым свойством квадрата – все его стороны абсолютно равны друг другу, поэтому квадрат называют правильной фигурой.
Существует вторая, более сложная формула для площади квадрата, в которой вычисления производятся с помощью диагонали. Диагональ – это линия, соединяющая два угла.которые противоположны друг другу. Чтобы найти площадь, нужно возвести длину диагонали в квадрат и разделить результат на два: S = ½ d 2 .
В случае с прямоугольником используется формула: S = a * b, где a, b – длины двух разных сторон, имеющих общую вершину.
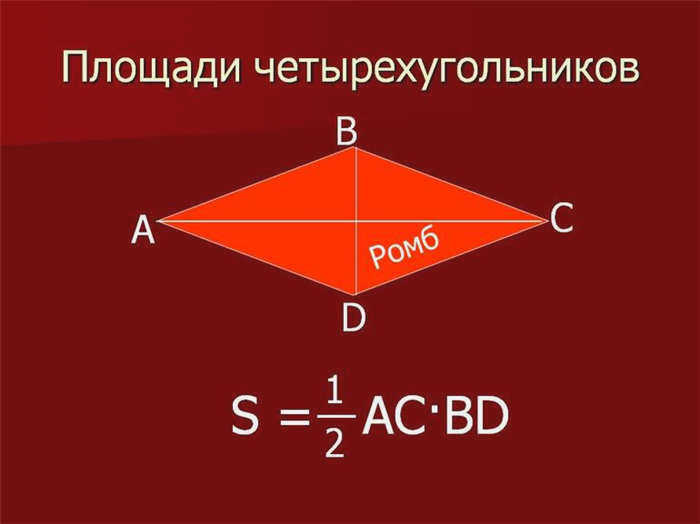
Параллелограмм, ромб и трапеция
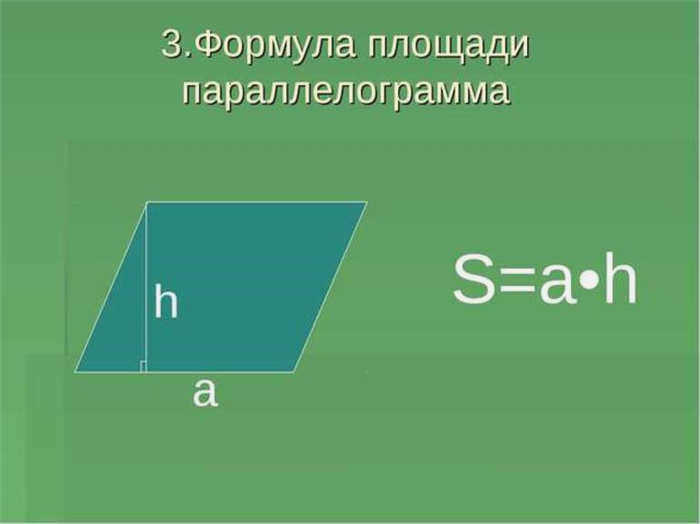
Параллелограмм – это четырехугольник с двумя противоположными тупыми и двумя острыми углами.
Для определения площади параллелограмма используются три формулы:
Круг и эллипс
Наиболее распространенная и широко используемая формула для определения площади круга заключается в умножении радиуса круга в квадрате на число пи: S = π * r 2 .
Число пи, обозначаемое греческой буквой "π", – это математическая константа, которая получается в результате деления окружности круга на его диаметр. π – это не поддающееся количественному измерению число. Для расчетов используется его среднее значение 3,14.
Вместо радиуса можно использовать диаметр окружности: диаметр возводится в квадрат, умножается на число π и полученный результат делится на четыре. Формула выглядит следующим образом: S = (π * d 2 ) / 4.
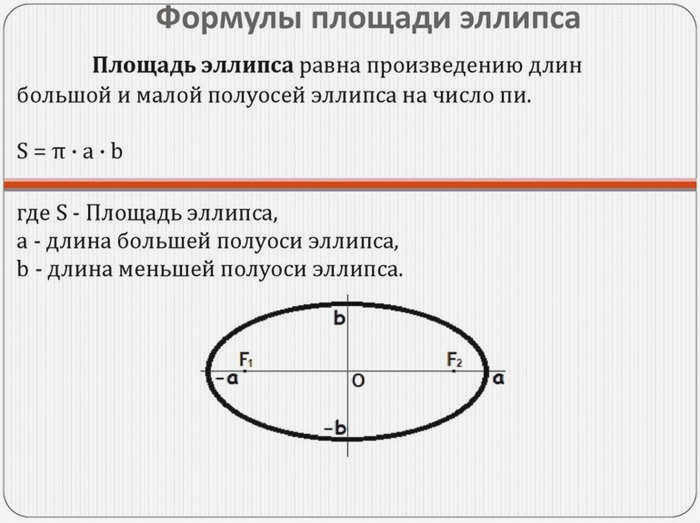
Чтобы вычислить площадь такой фигуры, как эллипс, необходимо провести две оси, то есть две линии, каждая из которых делит эллипс на две равные части так, чтобы сами линии были перпендикулярны друг другу (образовывали прямой угол). Точка пересечения делит каждую ось пополам, образуя полуось.
Площадь эллипса вычисляется как произведение трех величин: числа π, длины большой полуоси (a) и длины малой полуоси (b): S = π * a * b. Для вычисления площади различных фигур можно также использовать специальные онлайн-калькуляторы.
