Обычно люди сталкиваются с транспортирами в математике, когда учатся делать точные геометрические фигуры в школе. Возможно, многим из них никогда больше не придется использовать эти инструменты, но у транспортиров долгая история применения в различных областях.
Измерение углов
На предыдущем уроке мы узнали, что единицей измерения углов и дуг является градускоторый равен $$$ окружности. Поэтому измерение углов – это "процесс проверки" того, сколько частей окружности ($frac$) находится между сторонами угла.
Это дает ответ bона большинство заданных ранее вопросов, но не на все. Теперь, когда у нас есть единица измерения, нам нужно понять принципы, определяющие суть геометрии измерения углов.
Измерение углов – основные свойства
Начертите на плоскости угол $angle$ и проведите луч $AD$ между его сторонами $AB$ и $AC$. Предположим, что нам известна градусная мера $угла$ и $угольника$.
Сколько составляет угол $?
Мы помним аксиому, которая гласит, что длина отрезка равна сумме длин частей, на которые он делится любой точкой. Измерение углов также подпадает под аксиому "длины", только, конечно, вместо "длина"… мы будем говорить …показатель степени»:
$A_8$. Градусная мера угла равна сумме градусных мер углов, на которые он делится любым лучом, проходящим между его сторонами.
Геометрия измерения углов:
Измерение углов с помощью транспортира
Инструментом для измерения углов является транспортир. Он представляет собой пластину в форме круга или полукруга, иногда с линейкой в качестве основания. Полукруглый транспортир имеет 180 градусов, а круглый состоит из . 360. По сути, транспортир – это конечный результат идеи разделить круг на 360 равных частей и соответствующим образом обозначить окружность.
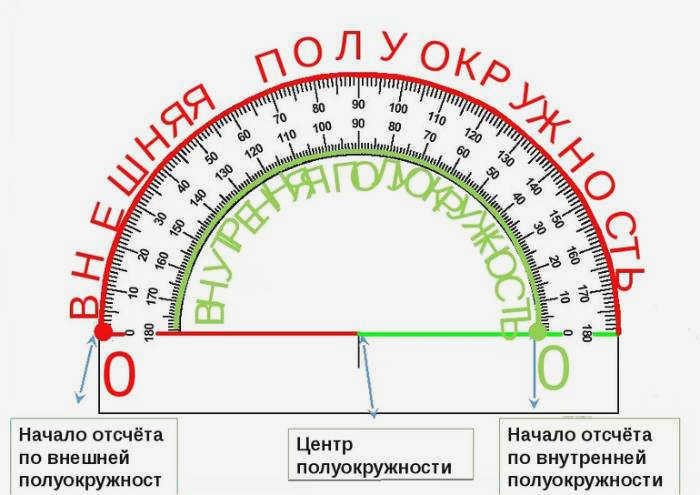
Полукруглый транспортир

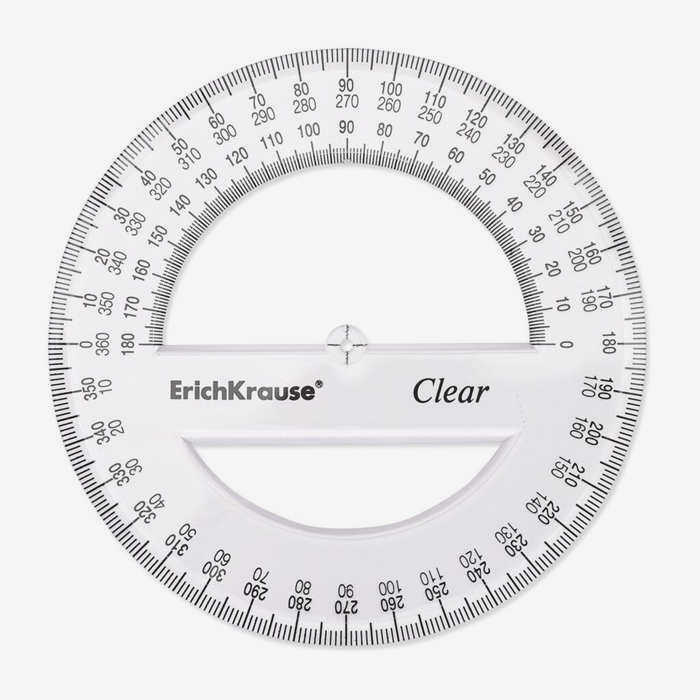
Круговой транспортир
Как использовать транспортир для измеренияй
Для измерения углов на уроках геометрии в школе хорошо подходит упрощенная версия транспортира – полукруглый транспортир. На самом деле транспортир используется не только для измерения, но и для построения углов. Прежде всего, мы рассмотрим, как измерение углов с помощью транспортира.
Шаг первый
Первым делом отметьте на базовой линии точку $A$, которая будет вершиной измеряемого угла. Из точки $A$ проведите луч, параллельный основанию транспортира. Первая часть угла определена.
✌️Определите вторую сторону угла
Для построения угла с помощью транспортира отметьте еще одну точку $80^rc$. Отметьте риску $80^rc$ маленькой вспомогательной точкой. Теперь проведите луч, проходящий через эту вспомогательную точку и точку $A$.
Обратите внимание, что обычно принято строить углы против часовой стрелки.. Альтернативная маркировка находится под основной маркировкой. по часовой стрелке – предлагается на транспортире, чтобы облегчить измерение углов. Ориентация углов на плоскости может быть разной, и не всегда полезно иметь под рукой маркер только против часовой стрелки.
^ ^circ$
Включает ли геометрия измерения углов нулевые значения? Оказывается, аксиома о сумме частей применима как к отрезкам, так и к углам. Но применима ли аксиома "….числа ноль…"? В отличие от отрезка, длина которого всегда строго больше нуля, мы можем говорить о нулевых углах. ..
Заметим, однако, что в некоторых учебниках используется следующая аксиома: "Каждый угол имеет градус, который больше нуля". Это не совсем верно, так как тригонометрические функции могут принимать аргумент равный нулю. Даже отрицательные аргументы.
Измерение углов – основные свойства: задача
Условие. Произведено измерение угла, которое дает следующие градусные меры: $угол=38^rc$, $угол=26^rc$, $угол=32^rc$.
Сколько градусов составляет $угол$?
Решение. Воспользуемся аксиомой о сумме градусных мер угла. То есть величина $угла$ будет определяться суммой величин составляющих его углов. А именно:
Градусные меры всех трех углов заданы условно. Остается только сложить их. Получаем следующий результат:
Ответ$96^rc$.
История изобретения
Истоки этого математического инструмента можно проследить до жрецов Египта и Вавилона, которые установили меры углов в градусах, минутах и секундах. Однако тригонометрия не использовалась в математике до классической Греции. Во втором веке до нашей эры астроном Гиппарх из Никеи изобрел тригонометрическую таблицу для измерения треугольников. Затем Птолемей включил в свою большую астрономическую книгу "Альмагейст" таблицу с угловыми приращениями от 0 до 180° с погрешностью менее 1/3600 единиц. Он также объяснил метод создания этой таблицы, и на протяжении всей книги приводил множество примеров того, как с ее помощью вычислять неизвестные элементы фигур. Птолемей также был автором так называемой теоремы Менелая для решения сферических треугольников, а его тригонометрия была основным учебником для астрономов на протяжении веков.
Возможно, в это же время индийские ученые разработали тригонометрическую систему, основанную на функции синуса, который, в отличие от используемого сейчас синуса, был не отношением, а длиной стороны, противоположной углу в прямоугольном треугольнике с данным противолежащим прямоугольником. Индийские математики использовали различные значения этой функции в своих таблицах. Томас Бландевиль описал инструмент, специально предназначенный для рисования и измерения форм, в своем "Кратком описании универсальных карт" от 1589 года. Как следует из названия, он использовал его для корректировки навигационных карт для использования в высоких широтах. Другие европейские математики также описали подобные инструменты примерно в то же время. Независимо от того, кто первым изобрел инструмент, к началу XVII века он стал стандартной практикой для мореплавателей и геодезистов. В 18 веке транспортиры стали появляться в учебниках геодезии и геометрии.
Транспортиры в современном понимании появились во второй половине 18 века, когда такие ученые, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали более ранние приборы.
Разновидности и применение
Угломер – это простой угломер, используемый для измерения или построения угла. Он выглядит как круглый или полукруглый диск с делениями. Циферблат может быть изготовлен из пластика, прочной бумаги или листового металла. Типичный диаметр составляет от 8 до 15 см, с делениями в 1° и 0,5°, когда также измеряется 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5°, в зависимости от диаметра шкалы. Более точные приборы имеют вращающуюся шкальную рейку (длиной до миллиметра).
Отчасти из-за разнообразного применения они производятся в различных формахПривычный полукруг, а также круги, прямоугольники, квадраты или квадранты. Они также могут иметь разный диаметр. Они изготавливаются из латуни, стали, дерева, слоновой кости или пластика. Наиболее распространенной формой является полукруг с градуировкой 180 градусов.
Угломер – это градуированный круглый инструмент с одним вращающимся рычагом; он используется для измерения или разметки. В строительстве часто требуется измерить угол в 90 градусов. Иногда в комплект входит шкала верньера для получения более точных показаний. Этот инструмент широко используется для архитектурных и механических чертежей, хотя его применение сократилось с появлением современных чертежных программ.
Универсальные транспортиры используются производителями инструментов; поскольку они производят измерения путем механического контакта с объектом, они классифицируются как механические транспортиры.
Угловой транспортир используется для измерения и проверки углов с очень жесткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0° до 360°.
В настоящее время также используются электронные приборы, которые обычно работают с поворотным энкодером. Также к транспортиру относятся:
Как это работает: линейки и шкалы
Если вы хотите понять, как измерять углы транспортиром, необходимо вспомнить, как он устроен. Вариант, знакомый большинству людей, представляет собой плоский полукруглый инструмент со следующими характеристиками:
- Его форму образуют две измерительные линейки: прямая линейка (внизу) и полукруглая линейка.
- Прямая линейка имеет обычную разметку (см, мм). Единственное отличие от стандартных линеек – выделенная точка, центр транспортира.
- Полукруглая линейка имеет шкалу (или две шкалы, вперед и назад), по которой определяется угол.
- Полукруглая шкала размечена с шагом 10°, с промежуточными делениями, что позволяет производить измерения с точностью до 1°.
- Две полукруглые шкалы перевернуты от 0° до 180° слева направо и наоборот для острых и тупых углов.

Манометр с двумя шкалами
Источник maped.one
Также распространены циркульные транспортиры в виде диска с прямой линейкой в центре и круговой шкалой, размеченной от 0° до 360°. Окружность всегда равна 360° (телесный угол), полуокружность измеряет 180° (вытянутая, наполовину заполненная). Соответственно, четверть окружности (и половина полной окружности) – это 90°, прямой угол.
Когда размер инструмента имеет значение
Длина прямой линейки составляет от 10 до 15 сантиметров. Это компактный и простой в использовании инструмент для простых чертежных задач. Однако у нее есть фундаментальное ограничение: она может измерять градусы угла, но не более точно. Другими словами, невозможно измерять с точностью 0,5° и более.
Решение заключается в увеличении размера транспортира. Чем он больше, тем точнее можно определить угловую линейку и измерить углы с точностью до половины градуса или даже больше.

Пример измерения острого угла
Источник mebpilot.com
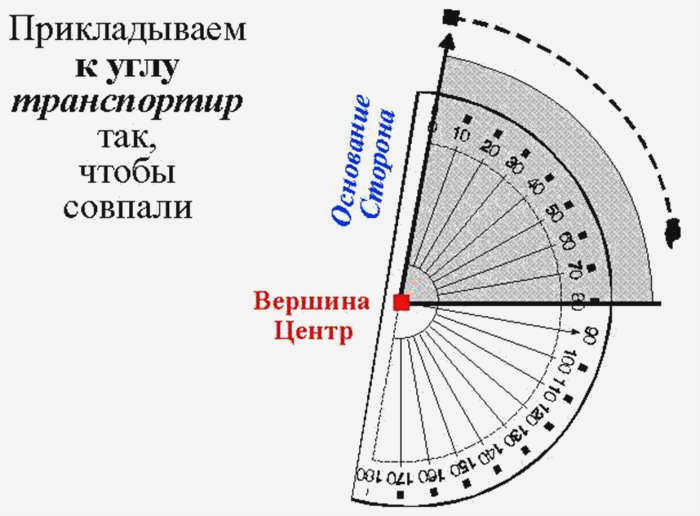
Построение угла
Я беру чистый лист бумаги квадратной формы. На нем карандашом отмечаю точку, от которой отходит прямая линия, являющаяся одной из сторон будущего угла. Эта линия используется для указания направления другой стороны. В простых упражнениях, чтобы научиться чертить углы, линия проводится горизонтально.
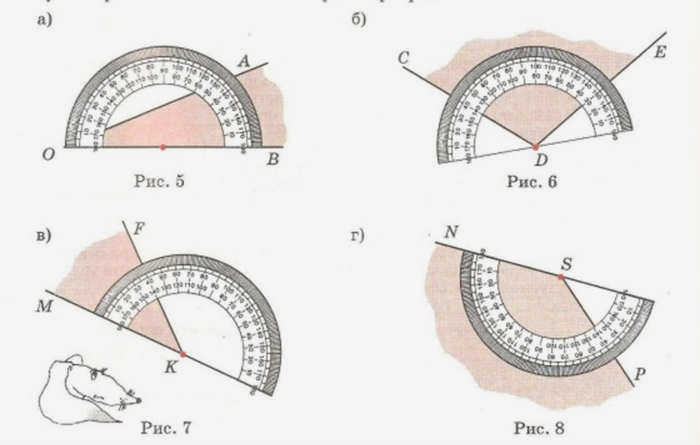
Центр основания транспортира располагается на обоих концах линии, которая будет вершиной угла. Эта точка отмечается на бумаге карандашом. К этой точке, внутри отверстия, прикладывается вершина угла, одна сторона которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.
Затем на шкале отмечается требуемый градус. На внутренней стороне отверстия также отмечается точка вблизи этого градуса. От вершины к этой точке проводится прямая линия. Таким образом, получается требуемый угол.
Для того чтобы правильно использовать транспортир очень важно выровнять егои точно применить его для получения правильных измерений.
Пересекающиеся линии в верхней части прямого края линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.
Измерение углов. Измеритель углов. Виды углов.
Мы знаем, что при измерении отрезков, мы сравниваем сравниваем измеренный отрезок с отрезком, который принимается в качестве единица измерения (1 мм, 1 см, 1 м и т.д.). Аналогично измеряются углы: для того, чтобы измерить угол сравнивается с с углом, который принимается за единица измерения – с градусзаписывается как 1°.
Степень измерения угла – это число, которое показывает во сколько раз градус и его части соответствие в данный угол.
Пример:

Градусная мера угла ABC равна  . Говорят: "Угол ABC равен 120 градусам". Сказано:
. Говорят: "Угол ABC равен 120 градусам". Сказано:  .
.

Угол – это измерительный инструменткоторый используется для измерения и строительство углов. Она состоит из линейка (линейка) и полукруга (угловая шкала: внутренняя и внешняя), которая делится на градусы от 0 до .
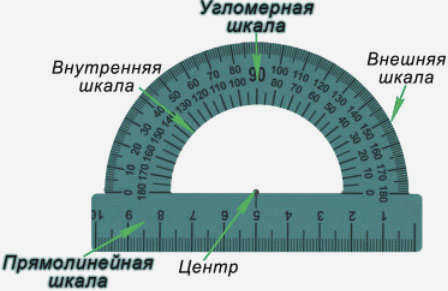
Для того чтобы измерить угол, необходимо выровнять вершину угла с центром транспортира, при этом одна сторона угла должна проходить через нулевую точку шкалы, и тогда вторая сторона угла укажет градус угол.
Измерение углов с помощью транспортира
Углы измеряются с помощью транспортира. транспортир:

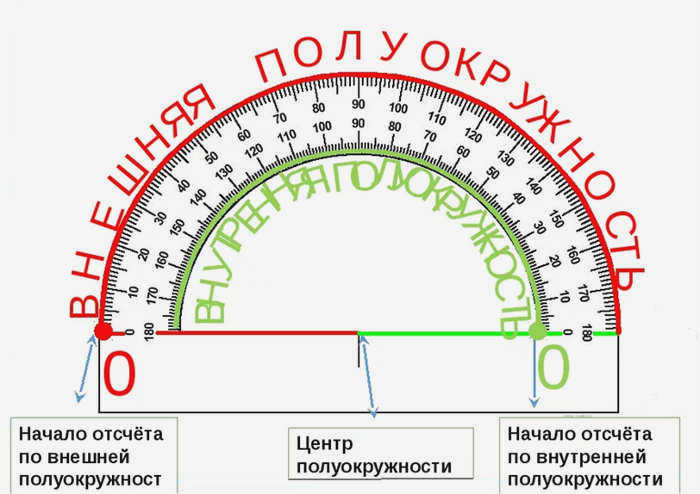
У транспортира есть две шкалы – внутренняя и внешняя. Внутренняя и внешняя шкалы начинаются с разных сторон. Чтобы получить правильные результаты измерения, отсчет градусов должен начинаться с правильной стороны.
Углы измеряются следующим образом: транспортир ставится на угол так, чтобы вершина угла совпадала с центром транспортира, а одна сторона угла проходила через нулевую отметку на шкале. Другая сторона угла будет указывать на величину угла в градусах:
Считается, что угол BOC равен 60 градусам, угол MON равен 120 градусам и записывается: ∠BOC = 60°, ∠MON. = 120°.
Для более точного измерения углов используются доли градуса: минуты и секунды. Минута – это угол, равный доле градуса. Секунда – это угол, равный доле минуты. Минуты обозначаются ‘ а секунды обозначаются ” . Знак минут и секунд располагается в правом верхнем углу числа. Например, если угол составляет 50 градусов, 34 минуты и 19 секунд, он записывается как :
Свойства измерения угла
Если луч делит данный угол на две части (на два угла), то значение этого угла равно сумме значений двух полученных углов.
Рассмотрим угол AOB:
Радиус OD делит его на два угла: ∠AOD и ∠DOB. Следовательно, ∠AOB = ∠AOD + ∠DOB.
Развернутый угол равен 180°.
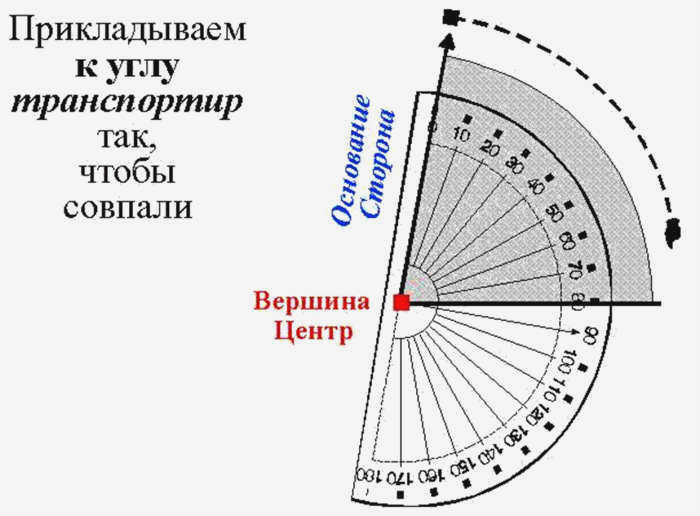
Каждый угол имеет конкретное значение, большее нуля.
