Диаметр окружности – это прямая, проведенная между двумя точками окружности и проходящая через центр окружности.
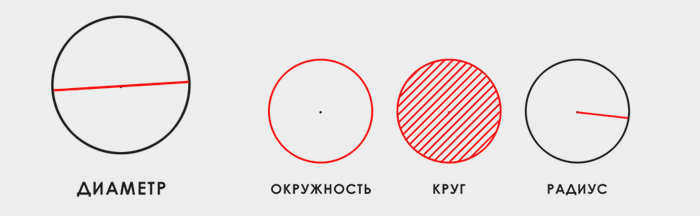
Прежде чем перейти к последовательности вычислений, важно понять разницу между этими понятиями.
Окружность – Замкнутая плоская кривая, все точки которой равноудалены от центра и лежат в одной плоскости.
Окружность – Окружность – это часть плоскости, лежащая внутри окружности, и сама окружность.
Проще говоря, круг – это замкнутая линия, такая же, как обод и велосипедное колесо. Окружность – это часть плоскости, ограниченная окружностью, например, блин или круг, вырезанный из картона.
Диаметр – линия, проведенная между двумя точками окружности и проходящая через ее центр.
Радиус – линия, соединяющая центр окружности с любой ее точкой.
Получайте советы, статьи, видео и контрольные списки по обучению в свой почтовый ящик

Узнайте, какие профессии будущего вам подходят
Пройдите тест, и мы покажем вам, кем вы могли бы стать, а также вышлем подробное руководство о том, как стать настоящим собой прямо сейчас.
Пройдите тест!

Как узнать диаметр. Узоры
В этой теме мы изучим три формулы:
1. общая формула.
Из основных определений мы знаем, что величина диаметра равна двум радиусам: D = 2 × R, где D – диаметр, а R – радиус.
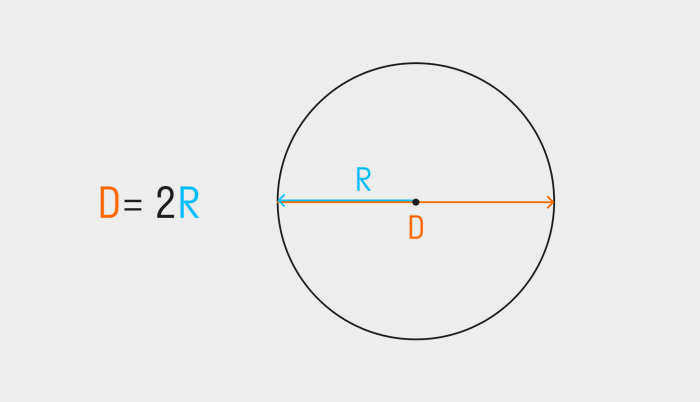
2. если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C – окружность, π – константа, равная отношению окружности к диаметру, всегда равна 3,14.
Чтобы получить правильный ответ, вы можете разделить на столбец или воспользоваться онлайн-калькулятором.

3. если у вас есть чертеж окружности
- Проведите прямую горизонтальную линию внутри круга. Положение линии не играет существенной роли.
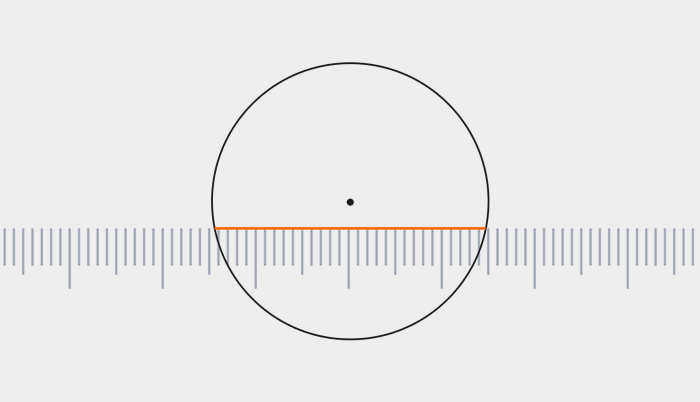
- Отметьте точки, в которых линия пересекает окружность.
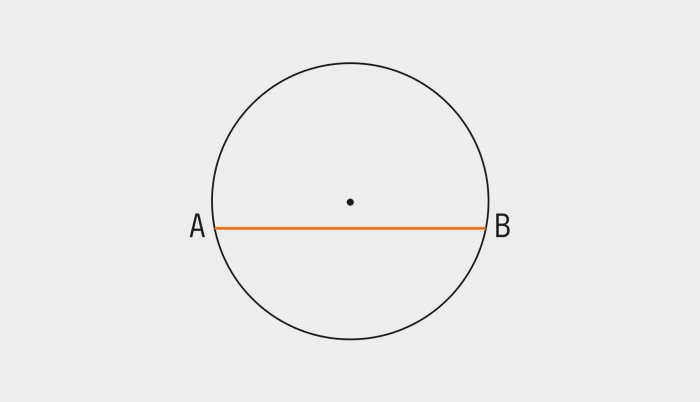
- С помощью компаса начертите две окружности одинакового радиуса (большего, чем радиус исходной окружности), первая с центром в точке A, вторая с центром в точке B.
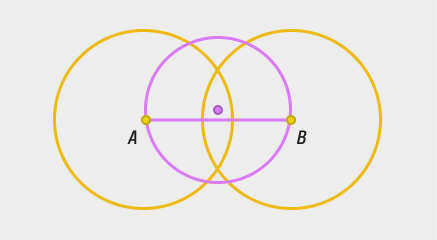
- Проведите линию через две точки пересечения. Отметьте точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
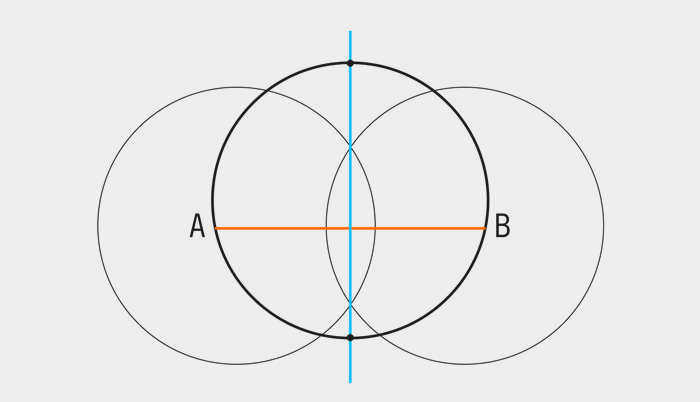
- Теперь измерьте диаметр окружности с помощью линейки. Готово!
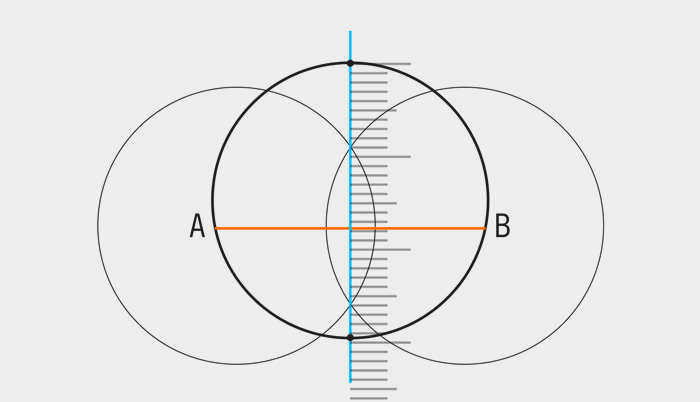
Формулы для определения диаметра окружности
Существует несколько различных способов определения диаметра в зависимости от известных частей окружности.
Радиус
Самая простая формула для определения диаметра может быть использована, если известен радиус окружности. Радиус – это отрезок, соединяющий центр окружности (или сферы) с любой точкой окружности. Диаметр равен двум радиусам.
Где d – диаметр, а r – радиус.
По длине окружности
Второй способ нахождения диаметра можно использовать, если известна длина окружности. Круг – это замкнутая плоская кривая, все точки которой равноудалены от центра. Поэтому диаметр равен длине окружности, деленной на число Pi.
Где d – диаметр, L – длина окружности, а π – константа, равная 3,14.
Эта формула основана на том, что отношение окружности круга к его диаметру всегда является постоянным числом, которое приблизительно равно 3,14 и называется π (пи).
По площади круга
Формула для вычисления диаметра по площади круга немного сложнее. С другой стороны, в большинстве случаев площадь круга вычисляется, если известен его диаметр. Но если задача обратная, то формула будет выглядеть следующим образом:
Где d – диаметр, S – площадь круга, а π – константа, которая приблизительно равна 3,14.
Это означает, что диаметр равен удвоенному корню из корня квадратного из площади круга и числа пи. Стоит отметить, что корень и мощность ½ – это одно и то же.
Примеры расчетов диаметров
Давайте рассмотрим несколько примеров, подтверждающих это.
Пример 1: Диаметр по длине окружности трубы 🚿.
Предположим, у вас нет под рукой штангенциркуля (прибора для измерения ширины изделий).

Вам нужно рассчитать диаметр существующей трубы, у которой нет конца. Для этого вы можете использовать рулетку или сантиметр, чтобы измерить длину окружности, просто обернув рулетку вокруг трубы. Затем разделите эту длину на 3,14. Если длина окружности трубы равна 31,4 сантиметра, то диаметр будет равен отношению этой длины к числу Пи, т.е:
d = 31,4 / 3,14 = 10 см.
Это и есть правильный ответ – 10 см.
Пример 2: диаметр зависит от радиуса окружности 🚲.
Здесь случай намного проще. Предположим, мы знаем радиус велосипедного колеса – 10 дюймов. Каков будет его диаметр?
Диаметр будет равен двум радиусам, или 20 дюймам.
Для сравнения, 1 дюйм = 2,54 сантиметра. Следовательно, 10 дюймов = 25,4 сантиметра. В результате диаметр окружности составляет: 2 × 25,4 = 50,8 см.
Площадь круга и размер пиццы
Люди не всегда правильно соотносят площадь круга с его диаметром. Например, можете ли вы ответить:

Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, потому что их радиусы составляют 50 см, что больше 40. Однако это неверный вывод, потому что сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 25 2 + 25 2 = 625 + 625 = 1250
- 40 2 = 1600
Поскольку ¼π – константа, сравнивать можно только квадраты диаметров. Получается, что пицца диаметром 40 см больше, чем 2 пиццы диаметром 25 см. Но если диаметр пиццы равен 35 см, то 35 2 = 1225, и в этом случае 2 пиццы диаметром 25 см будут иметь большую площадь.
Площади усеченных частей круга
Полезно также знать следующие геометрические элементы, связанные с окружностями и кругами:
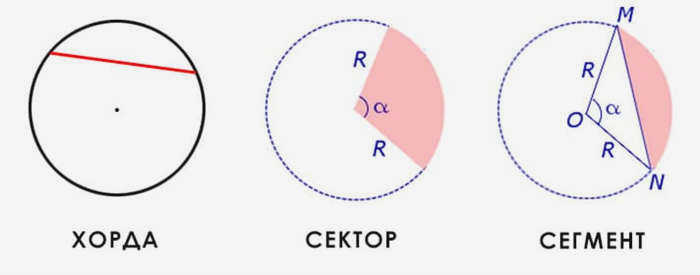
Хорда – Отрезок, соединяющий любые две точки окружности.
Сектор – часть круга, ограниченная дугой и двумя лучами, соединяющими концы дуги с центром круга.
Сектор – это часть круга, и его площадь связана с окружностью круга так же, как окружность сектора связана с окружностью всего круга. Поэтому площадь сектора равна площади круга, умноженной на отношение окружности сектора к окружности всего круга.
Площадь сектора можно рассчитать и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
где S – площадь сектора, а r – радиус круга.
Сегмент – это часть окружности, ограниченная дугой и соединяющей ее хордой.
Площадь сегмента можно найти по формулам:
где S – площадь сегмента, sinα – синус угла между двумя лучами к концам хорды, r – радиус круга.
Длина окружности или окружность круга
Найдите длину окружностиЧасто называемую окружностью круга, вам поможет наш калькулятор окружностей. Для расчета просто введите радиус или диагональ окружности и получите ответ онлайн. Мы также приводим формулы для самостоятельного вычисления окружности круга.
Окружность – Замкнутая плоская кривая, в которой все точки равноудалены от заданной точки (центра) и лежат в одной плоскости (называется радиусом окружности).
Прежде чем обсуждать расчет длины окружности, необходимо ознакомиться с основными понятиями. Нам необходимо понять значение терминов окружность, окружность, радиус и диаметр. Графически они представлены на диаграмме ниже.
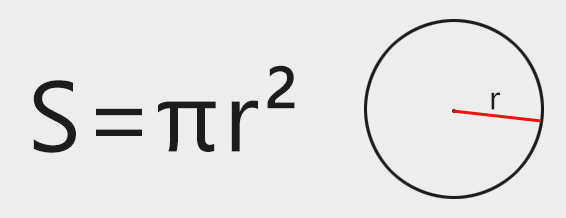
Примеры задач на определение длины окружности
Найдите длину окружности, если ее радиус равен 4,5 см.
Воспользуемся первой формулой. Подставьте радиус и вычислите окружность круга:
P = 2 Ò R = 2 Ò R = 2 Ò 4,5 = 9 Ò 9 Ò см.
Вы можете проверить результат с помощью калькулятора.
Найдите длину окружности диаметром 1,8 м.
В этом случае нам поможет вторая формула.
P = D = 1,8 D = 1,8 Dm.
