Оба полученных простых числа являются положительными, т.е. удовлетворяют нашим условиям. Зная b, мы можем легко найти a:

Обозначим площадь
Площадь a – это одно из свойств замкнутой геометрической фигуры, дающее нам информацию о ее размере. S (квадрат) – это знак площади.
Если размеры фигуры заданы в разных единицах, мы не сможем решить ни одной задачи. Поэтому для правильного решения задачи необходимо перевести все данные в одну единицу измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Получайте советы по обучению, статьи, видео и контрольные списки на свой почтовый ящик

Узнайте, какие профессии будущего вам подходят
Пройдите тест, и мы покажем вам, кем вы могли бы стать, и пришлем полезные советы о том, что вы можете сделать прямо сейчас.
Пройдите тест!

Круг
Окружность – это множество точек на плоскости, ограниченных окружностью, удаленных от центра на расстояние, равное радиусу. Радиусом обычно называют отрезок, соединяющий центр с любой точкой окружности.
- S = π × r 2 , где r – радиус, π – константа, равная отношению окружности круга к диаметру, она всегда равна 3,14.
- S = &pi × d 2 : 4; где d – диаметр.
- S = L 2 : (4 × π), где L – длина окружности.
Хотите быстро подтянуть свои знания перед экзаменом? Запишитесь на курсы ЕГЭ по математике в Skysmart!
Площади простых фигур
Формула для определения площади зависит от фигуры. Обозначение площади, чаще всего, остается неизменным – это заглавная латинская буква "S". Это не правило, а лишь одна из традиций написания площади поверхности. В высшей математике, теплотехнике и многих других дисциплинах площадь поверхности может обозначаться другими буквами.
Рассмотрим наиболее распространенные формулы для определения площади:
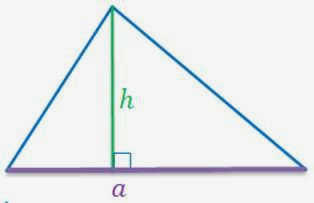
- Прямоугольник. S=a*b – произведение длины и ширины.
- Треугольник. $S=<1>over2>a*h$ – половина произведения основания на высоту, приведенную к этому основанию.
- Окружность. $S=<1>over2>r^2$ – отдельно отметим, что у круга не может быть площади. Только окружность.
Необходимо заранее убедиться, что параметры фигуры находятся в одних и тех же единицах измерения. Например, если ширина прямоугольника в миллиметрах, а длина в сантиметрах, переведите сантиметры в миллиметры и только потом используйте формулу.

Что такое площадь квадрата? Это сторона фигуры в квадрате. Потому что квадрат – это прямоугольник, длина и ширина которого равны:
Если у квадрата одна сторона равна 100 метрам, его площадь составляет один гектар. Эта единица измерения используется, когда необходимо оценить размер земельного участка при выделении сельскохозяйственных земель:
Площадь полей также может измеряться в акрах, которые в народе называют "сотками", поскольку один акр – это квадрат со стороной, равной 10 метрам, а его площадь, соответственно, равна $100$m^2$.
Площадь любой фигуры
Площадь составной фигуры можно определить, сложив площади ее частей. Для этого просто разделите любую геометрическую фигуру на простые части так, чтобы их площади можно было легко определить.
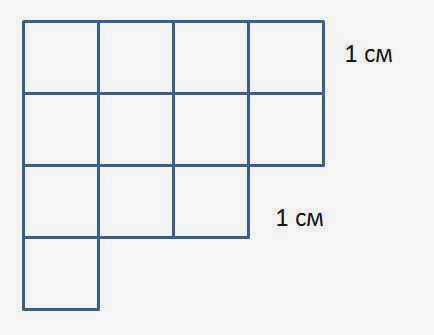
Фигуру на рисунке 3 можно разделить на 12 квадратов со стороной 1 см. Тогда площадь каждого квадрата будет равна 500 см^2$. Получается, что площадь данной фигуры будет равна 12 см^2$.
Связь между единицами измерения площади
Площадь измеряется в "квадратных" единицах: м 2 , см 2 , км 2 и т.д. Как эти единицы измерения связаны друг с другом? Чтобы ответить на этот вопрос, постройте квадрат со стороной 1 см и разделите каждую сторону на отрезки по 1 мм. Естественно, таких отрезков будет 10, так как 1 см равен 10 мм. Затем разделите большой квадрат на меньшие квадраты, число которых будет равно 10 2 = 100:
Площадь большого квадрата равна 1 см 2 , а площадь маленьких квадратов – 1 мм 2 . Поскольку большой квадрат состоит из 100 маленьких квадратов, мы можем записать:
Существуют специальные единицы площади, известные как ар (сокращенно а) и гектар (сокращенно га). Первый – это квадрат со стороной 10 метров, а второй – квадрат со стороной 100 метров. Верны следующие соотношения:
В частности, если стороны квадратов отличаются в 10 раз, то их площади отличаются в 100 раз. Ниже приводится быстрый метод преобразования единиц площади. Предположим, нам нужно перевести 1 квадратный километр в квадратные дециметры. Сначала вычислите, во сколько раз километр длиннее дециметра:
Задача. Площадь круга равна 24 см2 . Выразите это значение в мм 2 и м 2 .
Решение. Миллиметр в 10 раз меньше сантиметра, поэтому 1 см 2 равен 100 мм 2 :
Площадь прямоугольника
Еще с начальной школы известно, что площадь прямоугольника равна произведению его сторон. Давайте докажем этот факт, используя только свойства площади и формулу, которую мы вывели ранее для площади квадрата.
Возьмем любой прямоугольник со сторонами a и b. Затем мы добавим его к квадрату со стороной (a + b):
С одной стороны, площадь большого квадрата (со стороной a + b) равна (a + b) 2 . С другой стороны, он состоит из 4 частей, поэтому его площадь равна сумме (a + b) 2 .
Таким образом, мы доказали следующую теорему:
Задача. Найдите площадь прямоугольника со сторонами 5 и 8 см?
Решение. Достаточно перемножить эти числа:
Задача. Найдите площадь фигуры, изображенной на рисунке:
Решение. Разделите фигуру на несколько прямоугольников:
Затем подсчитайте площадь каждого прямоугольника отдельно:
Задача. Половина комнаты должна быть покрыта паркетным полом. Длина и ширина комнаты составляют 6 м и 5,5 м, а каждая паркетная доска имеет размер 30×5 см. Сколько паркетных досок нужно купить для ремонта?
Решение. В этом типе задач все длины должны быть выражены в одних и тех же единицах. Расшифруйте размеры комнаты:
