Другими словами, окружность – это множество точек, которые находятся на одинаковом расстоянии от центра окружности на длину радиуса окружности. Длина окружности – это длина кривой, образованной этим множеством точек и ограничивающей окружность. Это хорошо видно на рисунке выше.

Что такое диаметр окружности?
Диаметр окружности – это прямая, проведенная между двумя точками окружности и проходящая через ее центр.
Для других фигур диаметр – это максимальное расстояние между точками фигуры. Диаметр окружности не является исключением, так как это самый длинный отрезок, который можно провести внутри окружности.
Если вы нарисуете диаметр, он будет выглядеть следующим образом (выделено красным на диаграмме ниже).
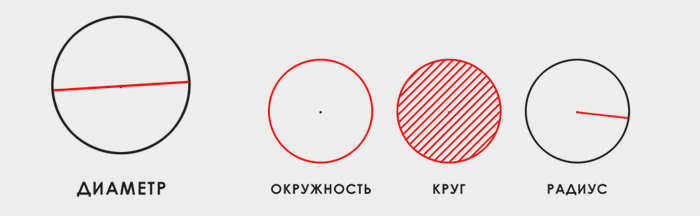
Теперь давайте рассмотрим, как можно найти диаметр и какие формулы для этого существуют.
Формулы для нахождения диаметра окружности
Существует несколько различных способов определения диаметра, в зависимости от известных частей окружности.
На основе радиуса
Самая простая формула для определения диаметра может быть использована, если известен радиус окружности. Радиус – это отрезок, соединяющий центр окружности (или сферы) с любой точкой окружности. Диаметр равен двум радиусам.
Где d – диаметр, а r – радиус.
По длине окружности
Второй способ нахождения диаметра можно использовать, если известна длина окружности. Окружность – это замкнутая плоская кривая, все точки которой равноудалены от центра. Поэтому диаметр равен окружности, деленной на пи.
Где d – диаметр, L – длина окружности, а π – константа, равная 3,14.
Эта формула основана на том, что отношение окружности круга к его диаметру всегда является постоянным числом, которое приблизительно равно 3,14 и называется π (пи).
Площадь круга
Несколько более сложной и запутанной является формула для вычисления диаметра по площади круга. В большинстве случаев, наоборот, необходимо вычислить площадь круга, если известен его диаметр. Однако если задача обратная, то формула будет выглядеть следующим образом:
Где d – диаметр, S – площадь круга, а π – константа, которая приблизительно равна 3,14.
Это означает, что диаметр равен удвоенному корню из корня квадратного из площади круга и числа пи. Стоит отметить, что корень и степень ½ – это одно и то же.
Как вычислить длину окружности?
Чтобы вычислить длину окружности, необходимо знать ее радиус, диаметр или площадь. Вам понадобится только один из этих элементов.
Диаметр
Диаметр – это линия, соединяющая две точки окружности и проходящая через центр окружности. Чтобы найти окружность круга по диаметру, просто умножьте диаметр круга на пи, чтобы получить его длину.
Формула будет выглядеть следующим образом:
Где L – окружность, π – константа, равная примерно 3,14, а d – диаметр.
Например, нам нужно рассчитать окружность канализационной трубы диаметром 100 мм. Окружность этой трубы можно рассчитать очень простым способом:
L = 3,14 × 100 = 314 мм.
Кстати, у труб есть 2 окружности и 2 диаметра: внутренний и внешний. Это хорошо показано на рисунке ниже.

Всегда обращайте внимание на то, какой диаметр известен, а какую окружность нужно рассчитать. Часто внутренний диаметр обозначается маленькой буквой d или D1, а внешний – просто D или DN.
Знание радиуса
Радиус окружности – это отрезок, соединяющий центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление окружности круга аналогично предыдущему: умножьте радиус на два и на пи, чтобы получить окружность.
Формула для расчета выглядит следующим образом:
где L – длина окружности, π – константа (приблизительно 3,14), а r – радиус.
Например, рассчитайте длину внутренней окружности трубы с внутренним радиусом 26 мм. В этом случае окружность получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что число Пи округляется до двух знаков после запятой, поэтому его всегда следует вычислять в пи и приводить как приближенное.
По площади круга
Самый редкий случай вычисления окружности круга – это когда нам известна только площадь круга. В этом случае для вычисления длины окружности можно использовать следующую формулу:
❓ Вопросы и ответы
В заключение предлагаем ознакомиться с ответами на некоторые часто задаваемые вопросы о вычислении окружности.
Что важнее: радиус, диаметр, длина окружности или площадь круга?
Площадь круга. И если расположить их все в порядке убывания, то рейтинг будет следующим:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие еще калькуляторы окружности доступны на сайте?
У нас есть много различных калькуляторовНапример, у нас есть калькуляторы для расчета диаметра, площади круга и окружности. Для последнего калькулятор окружности можно найти в верхней части этой страницы.
Почему число "пи" равно 3,1415926…. и не является "четным" числом?
Число пи – это отношение окружности круга к его диаметру. Вычислив его, математики обнаружили, что оно является не поддающимся количественному определению числом.Это означает, что его нельзя точно выразить в виде дроби m/n, где m – целое число, а n – натуральное число. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. По состоянию на июнь 2022 года известны первые 100 триллионов цифр числа "пи". Это точность, с которой можно вычислить площадь круга. В то время как квадрат и треугольник имеют точную площадь, круг всегда имеет приблизительную площадь.
Достаточно ли чего-то одного (диаметра, радиуса, площади), чтобы вычислить окружность круга?
Да, этого достаточно. Формулы и примеры вычисления окружности с помощью любого из них см. на вышеуказанной странице.
Что такое внутренняя и внешняя окружности? Чем они отличаются?
Внутренняя и внешняя окружности (как и диаметр) чаще всего используются для расчета характеристик труб, стенки которых имеют ненулевую ширину. Поэтому внутренняя окружность всегда меньше внешней. Обозначение L или LN используется для внешней окружности, а D или DN – для диаметра. Для внутренней окружности и диаметра добавляется нижний подстрочный индекс "один": L1 и D1или строчные буквы: l и d.
Как рассчитать диаметр. Формулы
В этой теме мы изучим три формулы:
1. общая формула.
Из основных определений мы знаем, что величина диаметра равна двум радиусам: D = 2 × R, где D – диаметр, а R – радиус.
2. если у нас возникла проблема с нахождением диаметра по длине окружности
D = C : π, где C – окружность, π – константа, которая равна отношению окружности к диаметру, всегда равна 3,14.
Вы можете разделить на столбец или использовать онлайн-калькулятор, чтобы получить правильный ответ.
3. если у вас есть чертеж окружности
- Проведите прямую горизонтальную линию внутри круга. Положение линии не играет существенной роли.
- Отметьте точку, где линия пересекает окружность.
- С помощью компаса начертите две окружности одинакового радиуса (большего, чем радиус исходной окружности), первая окружность с центром в точке A, вторая – с центром в точке B.
- Проведите линию через две точки пересечения. Отметьте точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Осталось только измерить диаметр окружности линейкой. И все готово!
Эти простые формулы пригодятся вам не только на уроках в школе, но и если вы захотите работать дизайнером интерьера, архитектором или модельером.
Какие диаметры бывают (+ таблица с размерами)?
Важно знать не только типы труб, но и их диаметры. Если при расчетах используются неверные данные, вся система может быть повреждена. Чтобы избежать типичных ошибок, важно ознакомиться со всеми правилами и терминами.
Использовать для расчетов только теоретические диаметры труб крайне непрофессионально. Да, это удобно и быстро, но ненадежно. Для того чтобы понять, как измерить диаметр, необходимо определить, какой параметр подлежит определению. Существует несколько значений, которые необходимы для правильных расчетов:
- Номинальный диаметр. Это размер трубы от стенки до стенки, измеряемый в миллиметрах. При использовании дюймовой системы измерения необходимо округление, что может негативно сказаться на точности результатов. Эта концепция необходима, когда несколько компонентов объединены, например, труба и фитинг.
- Толщина стенок играет значительную роль в точности расчетов. Это понятие облегчает определение прочности и надежности системы, расчет максимальных нагрузок и определение пригодности трубы для конкретного применения.
- Наружный диаметр – это внутренний диаметр, к которому добавлена толщина стенки.
- Номинальный диаметр – это эквивалент номинального отверстия, рассчитанного с помощью более точных методов.
Измерение диаметра трубы
Важно определить, в каких единицах измерения должен быть представлен результат. Это могут быть дюймы или миллиметры. Гораздо удобнее использовать метрическую систему. Такой подход позволяет более точно определить конечные характеристики полученной системы. Несмотря на это, чаще всего используется именно дюйм. Это облегчает округление результата, что упрощает задачу, но снижает точность цифр. Стоит отметить, что разница весьма незначительна. Для лучшего понимания полезно ознакомиться с размерами труб в дюймах и миллиметрах. Таблица позволит легко адаптировать и понять неизвестные размеры. Таблица диаметров стальных труб:
Зачем рассчитывать диаметр на основе окружности?
Как вариант, может быть дана площадь или окружность круга, в этом случае полезно иметь возможность вывести из нее диаметр или, для той же цели, определить радиус.

Пример: Вычисление диаметра из окружности
Вычислите диаметр, если известно, что окружность круга равна \n(3).
Ответ: Нам нужно найти диаметр \(d\) окружности, и из полученной информации мы знаем, что окружность круга равна \(C = 3\pi).
Теперь формула для окружности \(C = 2\pi), но так как диаметр равен удвоенной окружности, мы получаем \(d = 2\pi), и таким образом формула для окружности становится:
Приведенная выше формула показывает, как выразить окружность в терминах диаметра, и мы также можем решить формулу для \(d):
Все, что нам нужно сделать, это подставить известное значение цепи \(C = 3\) в приведенную выше формулу. Мы получаем следующий результат:
На этом расчеты завершены. Мы определили, что диаметр круга равен \(\displaystyle d = 3 \).
Пример: Отношение окружности круга к его диаметру
Если мы знаем, что окружность круга равна \n(4 \n), то каков его диаметр?
Ответ: Нам нужно найти диаметр круга \(displaystyle d), в этом случае мы знаем, что окружность круга равна \(C = 4).
Нам нужно воспользоваться формулой:
\[d = \displaystyle\frac <\pi>= \displaystyle\frac<\4\pi> <\pi>= 4\pi>].
Следовательно, диаметр равен \displaystyle d = 4.
Пример: Отношение окружности к диаметру
Предположим, что половина окружности равна \(\frac<3\pi> <3\pi>). Найдите диаметр окружности.
Ответ: В данном случае мы имеем дело не с окружностью, а с половиной окружности, т.е. \Ò(Òfrac<3Ò).
Другие калькуляторы окружностей
В математике круги встречаются повсюду. Вам понадобится вычислить площадь круга, окружность круга.
Кроме того, при работе с окружностями вам понадобится выполнить следующие преобразования углов, например, преобразование радианов в градусы или градусов в радианы.
Соответствующие калькуляторы
–>
